Abstract

The password has become today’s dominant method of authentication. While brute-force attack methods such as HashCat and John the Ripper have proven unpractical, the research then switches to password guessing. State-of-the-art approaches such as the Markov Model and probabilistic context-free grammar (PCFG) are all based on statistical probability. These approaches require a large amount of calculation, which is time-consuming. Neural networks have proven more accurate and practical in password guessing than traditional methods. However, a raw neural network model is not qualified for cross-site attacks because each dataset has its own features. Our work aims to generalize those leaked passwords and improves the performance in cross-site attacks.

In this paper, we propose GENPass, a multi-source deep learning model for generating ``general” password. GENPass learns from several datasets and ensures the output wordlist can maintain high accuracy for different datasets using adversarial generation. The password generator of GENPass is PCFG+LSTM (PL). We are the first to combine a neural network with PCFG. Compared with Long short-term memory (LSTM), PL increases the matching rate by 16%-30% in cross-site tests when learning from a single dataset. GENPass uses several PL models to learn datasets and generate passwords. The results demonstrate that the matching rate of GENPass is 20% higher than by simply mixing datasets in the cross-site test. Furthermore, we propose GENPass with probability (GENPass-pro), the updated version of GENPass, which can further increase the matching rate of GENPass.

Problem Description

When we talk about password guessing, we are not going to find a way to crack a specific password. We try to improve the matching rate between the training and testing sets. There are two types of tests in password guessing. One is called a one-site test, in which the training and testing sets are the same. The other is called a cross-site test, in which the training and testing sets are different. We have mentioned that all the previous work can only train and generate passwords based on one dataset, so their performance in cross-site tests is poor. However, a cross-site attack is the main technique for a hacker to crack a database.

On the other hand, many real passwords have been exposed but each dataset is not large enough for deep learning models. We believe if these datasets are combined together, the model can predict password more like a human.

In our work, we try to generate a “general” password list from several datasets to improve the performance of password guessing in cross-site tests. So we first define what is “general”.

General

Assume a training set T containing m leaked password datasets $D_{1}, D_{2}, D_{3},\cdots, D_{m}$ . Model $G_{t}$ is obtained by training T. Model $G_{i}$ is obtained by training $D_{i} (i \in \[1, m\])$ . If Model $G_{t}$ can guess dataset $D_{k} (D_{k} \notin D_{1}, D_{2}, D_{3}, \cdots, D_{m})$ better than $G_{i} (i \in \[1, m\]))$ , model $G_{t}$ is believed to be general.

Matching Rate

Suppose W is the wordlist generated by model G and the target dataset is D. We define the same passwords in both W and D as matched passwords. So the matching rate is the ratio between the number of matched passwords and that of D. Matching rate is $R_{G}$ .

$R_{G}=\frac{\left| W \cap D \right|}{\left| D \right|}$

Our model

PCFG+LSTM(PL)

A regular password guessing method called PCFG divides a password by units. For instance, ‘password123’ can be divided into two units ‘L8’ and ‘D3’. This produces high accuracy because the passwords are always meaningful and are set with template structures (e.g., iloveyou520, password123, abc123456). Meanwhile, neural networks can detect the relationship between characters that PCFG cannot. Thus, we combine the two methods to obtain a more effective one.

Preprocessing

A password is first encoded into a sequence of units. Each unit has a char and a number. A char stands for a sequence of letters (L), digits (D), special chars (S), or an end character (‘\n’), and the number stands for the length of the sequence (e.g., $Password123 will be denoted as S1 L8 N3 ‘\n’). Detailed rules are shown in Table [table1].

A table is generated when we preprocess the passwords. We calculate the number of each string’s occurrence. For example, we calculated all the L8 strings in Myspace, and found that ‘password’ occurred 58 times, ‘iloveyou’ occurred 56 times and so on.

Data Type	Symbols
Letters	ABCDEFGHIJKLMNOPQRSTUVWXYZ
Digits	0123456789
End character	\n
Special Chars	otherwise

[table1]Different string types

Generating

The LSTM model is a variant of the basic RNN model. We use LSTM to generate passwords. The structure of LSTM is exactly the same as. By feeding the LSTM model the preprocessed wordlist and training it, the model can predict the next unit.

Weight Choosing

When a unit is determined, it will be transformed back into an alphabetic sequence according to the table generated during the preprocessing. Experiments have shown that if the highest weight output is chosen each time, there will be a large number of duplicates in the output wordlist. So we choose the unit by sampling the discrete distribution. Such random selection can ensure that higher weight candidates are chosen with a higher probability, while lower ones can still be chosen after a large number of guesses.

GENPass

PL model is designed to improve the performance when we train only one dataset. However, it is not good enough when we train several datasets at the same time. So we propose GENPass to solve the multi-source training problem. GENPass generates a general wordlist from different datasets. Because different datasets have different principles and different lengths, it is difficult to learn the general principles by simply mixing datasets. To solve this problem, we design GENPass as shown in Fig 1. 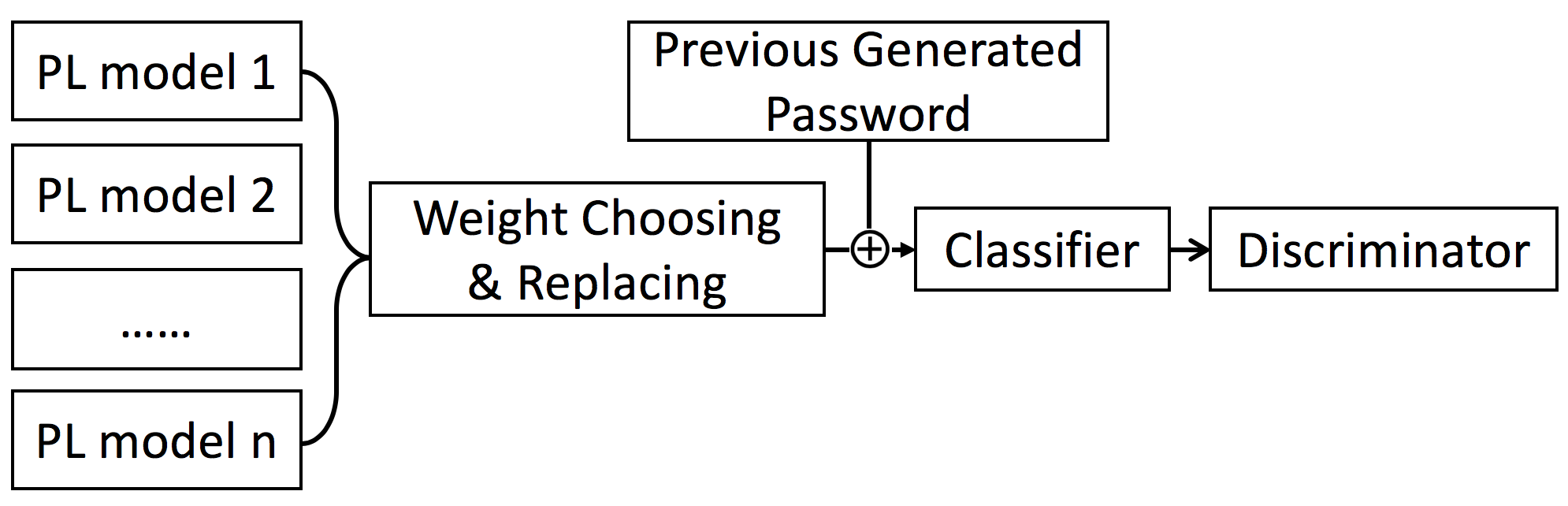avatar Fig 1. Diagram of GENPass model. Units are first generated by separate PL models. The weight choosing process selects one specific unit from these units. The unit then is replaced by a random sequence. The sequence together with the previous generated password will be fed into the classifier. The classifier will judge which model the input belongs to. The validity of the unit depends on the judgment by the discriminator. If the discriminator is not able to tell which model the unit comes from, the unit will be accepted. Otherwise, it will be rejected.

Prediction of Model n

All the models are PL models, as mentioned in the previous section. We train each model separately. Thus, given an input, the model can output the result with its own principle.

Weight Choosing

We assume that every model has the same possibility, so the output of each model can be combined directly. The combined list is the input of the weight choosing process, and the output is a random choice. When a unit is determined, it will be replaced by a random alphabetic sequence, according to the table generated in preprocessing. To show the process of weight choosing more clearly, an example is shown in Fig 2.

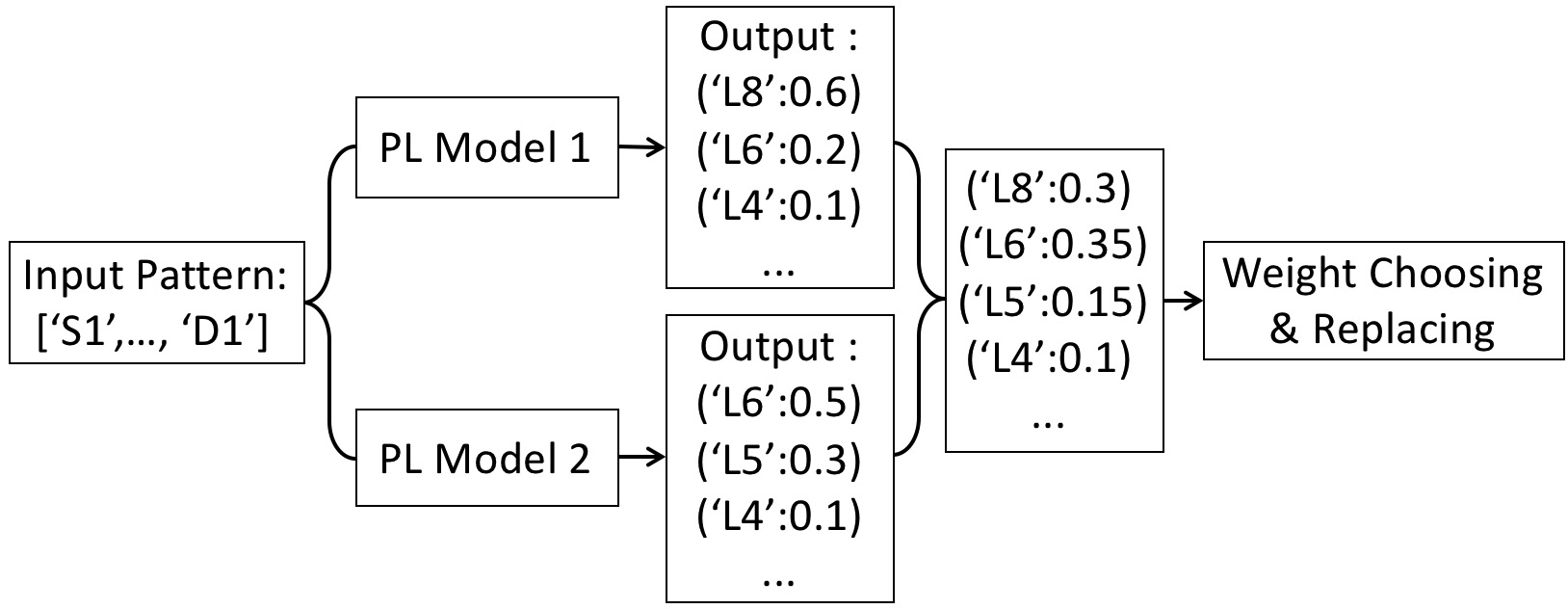avatar Fig 2. Example of weight choosing process. The output of Model 1 is [(L8:0.6), (L6:0.2), (L4:0.1)…] and The output of Model 2 is [(L6:0.5), (L5:0.3), (L4:0.1)…]. Because both models have the same possibility, we directly combine these two list. So the input for weight choosing can be written as [(L8:0.3), (L6:0.35), (L5:0.15), (L4:0.1)…]. Therefore, L6 is most likely to be picked out in weight choosing process. When a unit is determined, it will be replaced by a corresponding random sequence.

Classifier

The classifier is a CNN classifier trained by raw passwords without preprocessing from different datasets. Given a password, the classifier can tell which dataset the password most likely comes from. Through a softmax layer, the output will be a list of numbers whose sum is one.

The classifier only treats complete passwords, not units or alphabetic sequences. It means only when the end character ‘\n’ is generated, the classifier is activated. One single password is not long enough to extract features, we actually combine it with 4 previous generated complete passwords, 5 passwords over all, as the input to the classifier.

Discriminator

The discriminator is used to judge whether the password will be accepted. It takes the output of the classifier as its input. The discriminator should accept those passwords which have a consistent probability of appearance in different datasets so that the output passwords can be ‘general’. In other words, the distribution of the classifier’s output should be average.

We use C of the classifier’s output to judge the password’s generality.

Given the classifier’s output $c_{i}(i=1...N)$ where N is the amount of datasets, we define C as below.

$C=\sqrt{\frac{1}{N}\Sigma_{i=1}^{N}(c_{i}-\overline{c})^{2}}$ $\overline{c}=\frac{1}{N}\Sigma_{i=1}^{N}c_{i}$

If C is too large, the lately generated unit will be discarded because it is probably a special case in one dataset. Otherwise, the unit will be accepted. In our model, we chose 0.2 as the threshold of C after performing several experiments. If the threshold is too small, the model will be much more time-consuming and the output will contain more duplicates.

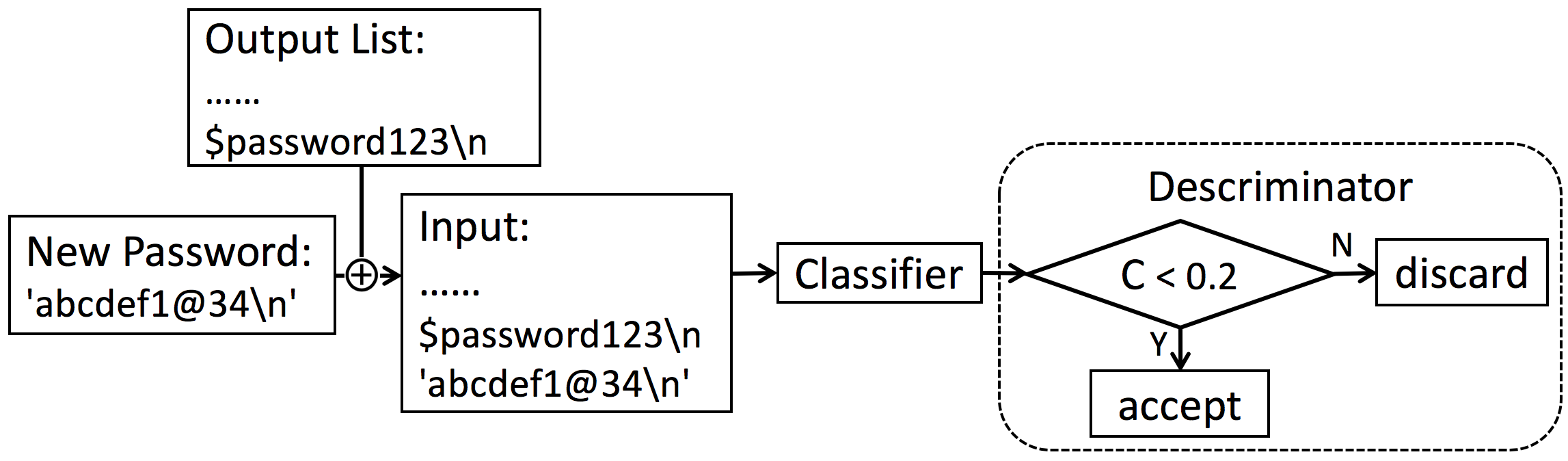avatar Fig 3. Detailed diagram of the classifier and the discriminator. Assume that the new generated password is ‘abcdef1@34’. It will be combined with 4 previous generated passwords as the input of the classifier. If the output of the classifier is [0.4,0.6], the discriminator will accept and print the password, because C is less than 0.2. If the output of the classifier is [0.3,0.7], all the units composing ‘abcdef1@34’ will be discarded.

GENPass with Probability

In the previous section, we assume that each dataset has the same probability. However, after some experiment we find some datasets are more typical, and passwords are more likely to come from those datasets, so we need to lower the opportunity for passwords from those typical datasets to be chosen to allow passwords from other datasets to have a greater chance of being selected. We introduce the concept of weights to solve this problem. Those typical datasets should have a low weight, which will be proven later. We develop a method to calculate appropriate weights. The generality is judged by whether the weight of datasets corresponds with the distribution of the classifier’s output. We improve the weight choosing process and discriminator in the previous model as follows. We call this upgraded model GENPass with probability, GENPass-pro for short.

Weight Choosing Process with Probability

We assume that a probability distribution P represents each dataset’s weight, where $\Sigma p = 1$ . So the outputs of different models should be added according to their weights. The weights are the probabilities. According to the Bayes formula, the total probability of the output is 1.

Discriminator with Probability

Generality is judged by the distance between the weight of datasets P and the distribution of the classifier’s output Q. Standard deviation cannot depict the distance between two distributions, so we introduce Kullback-Leibler divergence (KL divergence) to depict distance. The KL divergence is calculated as follows.

During the training process, we use gradient descent to force P to approach Q. The distribution P is first generated randomly. In each iteration, ten new passwords are generated by GENPass with corresponding probability. These passwords are fed to the classifier and the results are recorded as $Q_{i} (i=1...10)$ . We denote the average of these results as the output of the classifier Q to eliminate random error. We use KL divergence as the loss function. Updating P by ascending Q-P stochastic gradient times steps $\alpha$ makes P approach Q quickly and accurately. We assume steps of $\alpha=1$ . We use $P^{'}_{i} = \frac{P_{i}}{\Sigma{P_{i}}}$ to ensure the total probability is 1. We believe the distribution is stable when the loss is less than 0.001. The pseudo code is shown in the following picture.

When P is determined after training, the criterion for accepting the password is whether the KL divergence is smaller than 0.1, a value we set manually.

avatar

Fig 4. The algorithm of distribution calculatation